PERSAMAAN KUADRAT
Hallo teman-teman, pada kesempatan ini saya akan membagikan materi SMA mengenai persamaan kuadrat.
Yuk kita sama-sama mempelajarinya...
PERSAMAAN KUADRAT
1. Bentuk Umum Persamaan Kuadrat
Persamaan kuadrat adalah persamaan yang mempunyai bentuk umum
Dapat dilakukan dengan 3 cara :
a. Pemfaktoran
b. Melengkapi Kuadrat Sempurna
Jika tidak dapat difaktorkan, maka persamaan kuadrat dapat diselesaikan dengan melengkapkan kuadrat sempurna.
c. Menggunakan Rumus abc
Jika kedua cara diatas tidak dapat digunakan, maka cara terakhir untuk memecahkan soal persamaan kuadrat adalah dengan menggunakan rumus abc. Langkah-langkah :
1. Persamaan kuadrat ditulis dalam bentuk baku ax^2 + bx + c = 0
2. Menentukan nilai a,b dan c
3. Masukkan ke dalam rumus abc
3. Jumlah Dan Hasil Kali Akar-Akar
Jika X1 dan X2 akar-akar persamaan kuadrat ax^2 + bx + c = 0, maka :
X1 + X2 = -b/a
X1.X2 = c/a
4. Jenis-Jenis Akar Persamaan Kuadrat
Jenis dan banyaknya akar suatu persamaan kuadrat ditentukan oleh b^2-4ac. Bentuk b^2-4ac disebut Diskriminan yang dinotasikan dengan "D". Terdapat 3 kemungkinan diskriminan yaitu :
a. Jika D>0 persamaan kuadrat mempunyai dua akar real yang berlainan.
b. Jika D=0 persamaan kuadrat mempunyai dua akar real yang sama.
c. Jika D<0 persamaan kuadrat tidak mempunyai dua akar real atau kedua akarnya merupakan bilangan imajiner.
5. Bentuk Simetri Akar-Akar Persamaan Kuadrat
Bentuk simetri akar-akar persamaan kuadrat adalah bentuk dari akar-akar yang tidak berubah apabila X1 dan X2 betukar tempat. Bentuk Simetri akar-akar persamaan kuadrat terdiri dari :
6. Menyusun Persamaan Kuadrat
Untuk menyusun persamaan kuadrat yang akar-akarnya diketahui mempunyai hubungan dengan akar-akar persamaan kuadrat yang lain, dapat dilakukan dengan menggunakan rumus jumlah dan hasil kali akar-akar persamaan kuadrat tersebut, dengan langkah-langkah sebagai berikut.
contoh
Okey teman-teman.. mungkin hanya sedikit yang saya bagikan kepada teman-teman, semoga ini dapat membantu pemahaman teman-teman.. hehe
SUMBER : BUKU AMPUH RANGKUMAN MATERI SMA
KARANGAN : ISTIQOMAH RIAEDY, dkk
Yuk kita sama-sama mempelajarinya...
PERSAMAAN KUADRAT
1. Bentuk Umum Persamaan Kuadrat
Persamaan kuadrat adalah persamaan yang mempunyai bentuk umum
ax^2 + bx + c = 0
di mana a, b, c bilangan real, dan a tidak samadengan 0 , dan x adalah variabel.
Akar persamaan kuadrat adalah nilai pengganti x yang memenuhi persamaan kuadrat tersebut. Jika kita misalkan akar-akar persamaan kuadrat x1 dan x2 maka :
2. Menyelesaikan Persamaan KuadratDapat dilakukan dengan 3 cara :
a. Pemfaktoran
Jika tidak dapat difaktorkan, maka persamaan kuadrat dapat diselesaikan dengan melengkapkan kuadrat sempurna.
Jika kedua cara diatas tidak dapat digunakan, maka cara terakhir untuk memecahkan soal persamaan kuadrat adalah dengan menggunakan rumus abc. Langkah-langkah :
1. Persamaan kuadrat ditulis dalam bentuk baku ax^2 + bx + c = 0
2. Menentukan nilai a,b dan c
3. Masukkan ke dalam rumus abc
3. Jumlah Dan Hasil Kali Akar-Akar
Jika X1 dan X2 akar-akar persamaan kuadrat ax^2 + bx + c = 0, maka :
X1 + X2 = -b/a
X1.X2 = c/a
Jenis dan banyaknya akar suatu persamaan kuadrat ditentukan oleh b^2-4ac. Bentuk b^2-4ac disebut Diskriminan yang dinotasikan dengan "D". Terdapat 3 kemungkinan diskriminan yaitu :
a. Jika D>0 persamaan kuadrat mempunyai dua akar real yang berlainan.
b. Jika D=0 persamaan kuadrat mempunyai dua akar real yang sama.
c. Jika D<0 persamaan kuadrat tidak mempunyai dua akar real atau kedua akarnya merupakan bilangan imajiner.
5. Bentuk Simetri Akar-Akar Persamaan Kuadrat
Bentuk simetri akar-akar persamaan kuadrat adalah bentuk dari akar-akar yang tidak berubah apabila X1 dan X2 betukar tempat. Bentuk Simetri akar-akar persamaan kuadrat terdiri dari :
6. Menyusun Persamaan Kuadrat
Untuk menyusun persamaan kuadrat yang akar-akarnya diketahui mempunyai hubungan dengan akar-akar persamaan kuadrat yang lain, dapat dilakukan dengan menggunakan rumus jumlah dan hasil kali akar-akar persamaan kuadrat tersebut, dengan langkah-langkah sebagai berikut.
contoh
Okey teman-teman.. mungkin hanya sedikit yang saya bagikan kepada teman-teman, semoga ini dapat membantu pemahaman teman-teman.. hehe
SUMBER : BUKU AMPUH RANGKUMAN MATERI SMA
KARANGAN : ISTIQOMAH RIAEDY, dkk



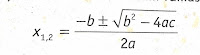






Tidak ada komentar:
Posting Komentar